
삼 각 함 수
아아.. 결국 수포자인 내가 삼각함수를 배워야 하는 순간이 왔다.
챌린지반의 수업 중, 발표 자료를 준비하라는 것이 출발이었지만,
언젠가는 배워야 할 것이었다.
따라서, ppt 에 정리한 내용을 바탕으로 TIL을 작성하였다.

수학 지식이 전무한 (흑흑) 나는 삼각함수를 배우기 전에 삼각형 부터 배워야한다...
초 등 학 생
삼각형이란,
3 개의 직선으로 이루어진 도형으로,
세 내각 의 합이 180도 이다 !

다음으로는 , 삼각비를 알아야 하는데,
앞으로 등장할 삼각형은 모두 직각 삼각형으로 설명한다는것을 기억하자.
중 학 생

(마지막으로 본게 20년은 된거같은데..)
삼각비는 , 위에 서술한 것 처럼, 삼각형의 두 변을 묶어서 비율로 나타낸 것이다.
여기서,
빗변이란, 직각 삼각형에서 가장 길이가 긴 변을 말하며,
직각을 이루는 두 변을 제외한 나머지 하나의 변이 된다. = 직각과 마주보는 변
특정한 각 A를 기준으로 직각을 이루는 쪽으로 가는 변이 밑변이 되고,
빗변과 밑변을 제외한 남은 하나의 변을 높이라고 표현한다.
주의사항으로,
언뜻 보기에 가로로 되어있다고 밑변, 세로로 되어있다고 높이 라고 하는것을 틀릴 수 있음에 주의 !!

추가적으로 tan A = sin A / cos A 로 표현할 수 있다.
(높이 = sin A * 빗변의 길이)
(밑변 = cos A * 빗변의 길이)

특수각은 간단히만 정리하고 넘어가도록 하자.
비교적 깔끔하게(?) 삼각비를 표현 할 수 있는 각들을 특수각 이라고 부른다.
경우에 따라 120 도, 150 180 210 ... 막 아무거나 집어넣는 모양인데...
우리는 0 30 45 60 90 도 만 기억하면 된다.
tan 30도를 루트3 /3 으로 표현하고 있는게 마음에 안들기 때문에,
1 / 루트3 으로 표현하는 쪽이 가독성이 더 좋다.
본격적으로 삼각함수를 들어가기....전에 마지막으로 호도법을 알아보자

호도법은 각도를 표현하는 방식중 하나이며,
깊이 들어가면 내용이 엄청 심오한듯 보이기 때문에, 필요한 부분만을 우선 이해하자. (수학은 늘 이런식이야)

우리가 평소에 사용하는 각도는
육십분법 에 해당하며 , 한바퀴의 회전을 360도 로 표현하는 방식이다.
그렇다면, 호도법은 위에서 나온 바와 같은데,
기억해야할 것은 180도 = 𝝿 (3.141592.......) 라는 것 !
왜 또 굳이 무리수인 파이를 가져와서 정의를 내린것인지 의문이 들지만

기존 육십분법의 각도와 달리
어떻게든 단위를 제거하고 숫자로 각도를 표현하기 위해 만든 표현법이라고 보면 될 듯 하다.

이게 대체 뭐람
깊이 들어가려면 심연을 봐야 하는 느낌이 강하게 들기 때문에,
일단 호도법 => 180도 = 𝝿 하고 넘어가도록 했다.
자.. 그럼 이제 삼각함수이다.

고 등 학 생
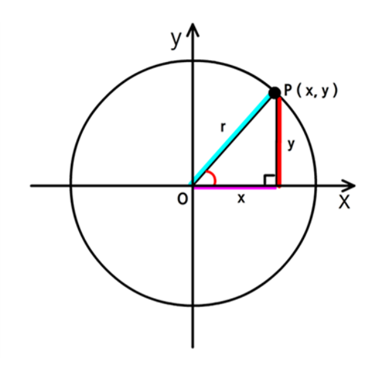
고등학생이 된 우리는
이제부터는 삼각형을 그리기 전에 십자가 + 를 먼저 그려야한다.
이 말은, 좌표가 생겼다는 말이고,
좌표를 통해 마이너스의 값을 표현 할 수 있게 되었다.
마이너스 좌표의 삼각형을 그리는 것으로
우리는 세타 가 90도가 넘는 (둔각) 삼각 함수의 값을 구할 수 있게 된 것이다 !!!!!!!
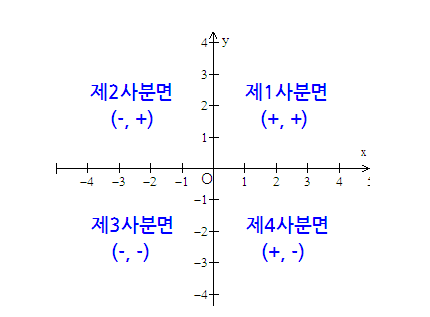
사분면에 관한것은 중학교 과정에 있다.
삼각 함수도 당연히 위와 마찬가지 이다.
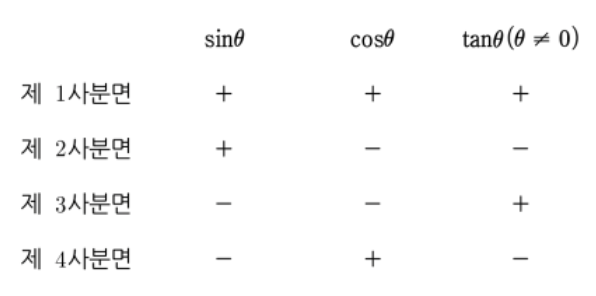
크게 어려운 내용은 아니지만,
쉽게 이해하려면 아래의 그림을 보자...
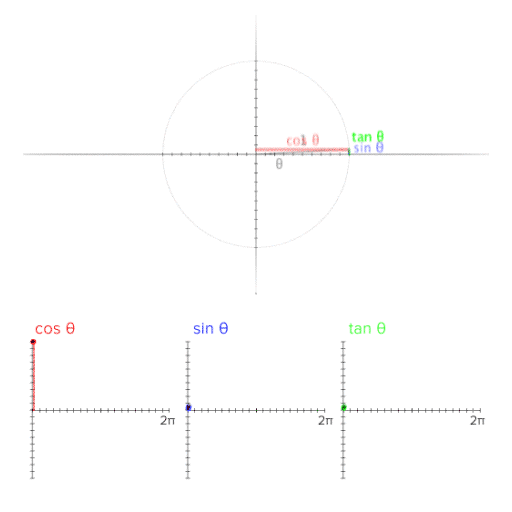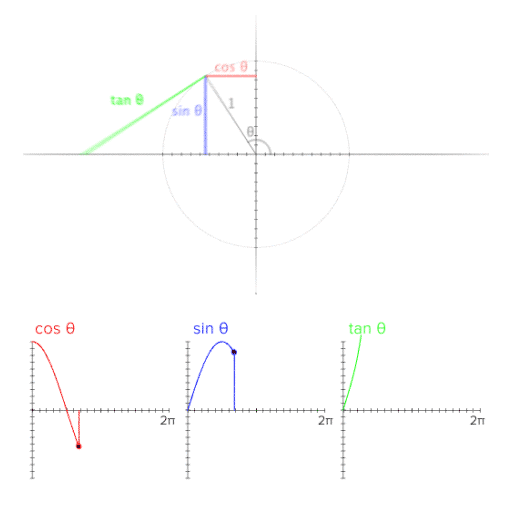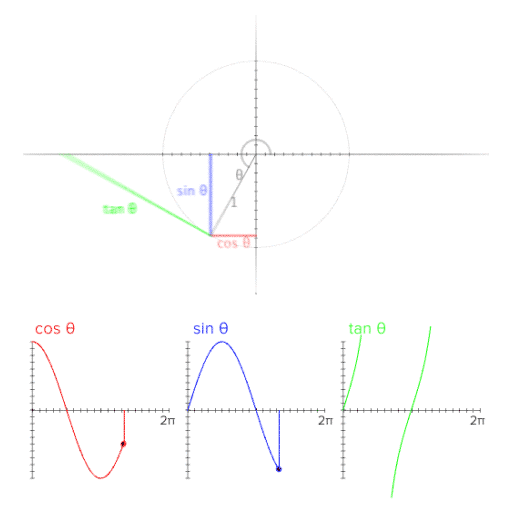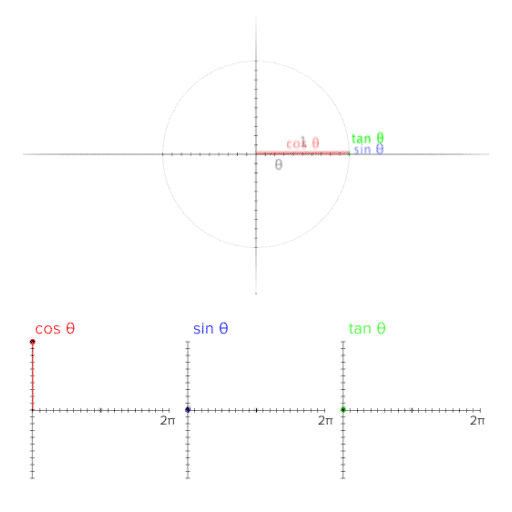
(0, 0)을 원점으로 r = 1 인 단위원을 양의 방향으로 그린다면
그림과 같은 형태를 볼 수 있다.
이걸 움직이는 그림으로 볼 수 있다니... 세상이 많이 좋아졌다 !!
보는것 처럼, 임의의 P 좌표의 위치에 따라
sin 세타와 cos 세타가 양수와 음수의 영역을 넘나드는 것을 볼 수 있고,
이를 그래프로 표현하는것 또한 확인할 수 있다.
위 그래프 에서는 한바퀴 (360도 = 2파이) 에 해당하는 지점만 표기되어 있지만,
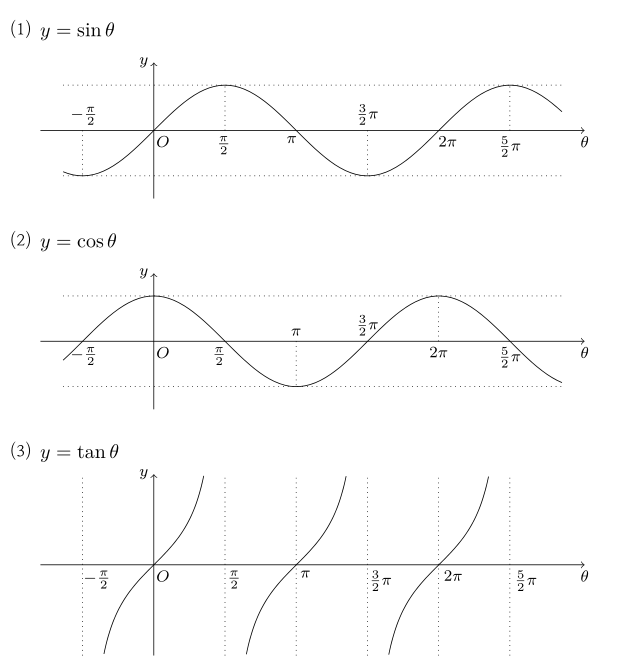
위 처럼 0도, 90도, 180도, 270도 마다 호도를 표기하여 본다면
어느 사분면에 위치한 삼각 함수 인지를 좀 더 쉽게 파악할 수 있다.
오늘은 여기까지...

'내일배움캠프' 카테고리의 다른 글
| 타워 디펜스 온라인 - 회고 (0) | 2024.11.12 |
|---|---|
| 24.11.01 TIL 멀티플레이 과제 트러블슈팅 (0) | 2024.11.01 |
| 24.10.24 TIL 위치 동기화 (0) | 2024.10.24 |
| 24.10.23 TIL 기본 세팅 (0) | 2024.10.23 |
| 24.10.18 TIL 버퍼 객체 (0) | 2024.10.18 |